Un effetto particolarmente interessante presente in molti videogiochi è la deformazione degli specchi d’acqua in reazione al movimento del giocatore o alla caduta di oggetti.

In questo articolo vedremo come realizzare un effetto di questo tipo in Unity, analizzando alcune soluzioni possibili.
Le basi – un sistema a molle
Nella vita reale il movimento dei fluidi è un argomento parecchio complesso. Riprodurlo fedelmente richiede tecniche avanzate di simulazione. Questo, a sua volta, implica un utilizzo intenso di risorse computazionali per un risultato che in molti casi non vale la pena ricercare.
In questo articolo esamineremo una tecnica alternativa, usatissima in molti giochi 2D di successo, basata sulle molle.
Nella vita reale, le molle sono oggetti di tipo elastico: se una molla viene allungata e poi lasciata libera, tornerà alla sua lunghezza originale.
La legge fisica che descrive il comportamento dei materiali elastici è la legge di Hooke.
Essa afferma che un corpo elastico subisce una deformazione direttamente proporzionale allo sforzo a esso applicato. In formule, questo equivale a dire:
$$F=-k\cdot\Delta x$$
Dove \(F\) è la forza elastica, \(k\) è la costante elastica e \(\Delta x\) è l’allungamento o l’accorciamento della molla rispetto alla posizione di riposo.
Una molla, dopo essere stata allungata, in assenza di smorzamento non solo ritorna alla propria lunghezza originaria, ma addirittura la supera per via della forza accumulata. Se non ci sono forze esterne che agiscono sulla molla, questa comincerà ad allungarsi e ad accorciarsi in un ciclo infinito, in un modo oscillatorio.
Questo è perfetto per i nostri scopi: vogliamo infatti simulare le onde attraverso una lunga fila di molle che reagiscono a forze esterne deformando la superficie dell’acqua.
Setup: creiamo la mesh
Il nostro obiettivo è avere una mesh generata in maniera dinamica che possa essere modificata dalla compressione e dilatazione delle molle.
La mesh in questione è molto semplice: un piano 2D, suddiviso un numero arbitrario di volte.
private void generateMesh() {
Mesh mesh = new Mesh();
Vector3[] vertices = new Vector3[(resolution + 1) * 2];
int[] triangles = new int[resolution * 6];
Vector2[] uv = new Vector2[vertices.Length];
for(int x = 0; x <= resolution; x++) {
int index = x * 2;
float normalizedX = (float)x / resolution;
vertices[index] = new Vector3(normalizedX, 0, 0);
vertices[index + 1] = new Vector3(normalizedX, 1, 0);
uv[index] = new Vector2(normalizedX, 0);
uv[index + 1] = new Vector2(normalizedX, 1);
}
int triangleIndex = 0;
for(int x = 0; x < resolution; x++) {
int bottomLeft = x * 2;
int topLeft = bottomLeft + 1;
int bottomRight = bottomLeft + 2;
int topRight = bottomLeft + 3;
triangles[triangleIndex++] = bottomLeft;
triangles[triangleIndex++] = topLeft;
triangles[triangleIndex++] = topRight;
triangles[triangleIndex++] = bottomLeft;
triangles[triangleIndex++] = topRight;
triangles[triangleIndex++] = bottomRight;
}
mesh.vertices = vertices;
mesh.uv = uv;
mesh.triangles = triangles;
mesh.RecalculateNormals();
mesh.RecalculateBounds();
GetComponent<MeshFilter>().mesh = mesh;
}Il codice in questione crea un piano con un numero di suddivisioni pari al valore della variabile resolution
I vertici su cui lavoreremo sono i vertici superiori
Creiamo le molle
Iniziamo specificando 3 variabili:
public int springsCount: il numero di molle uniformemente posizionate lungo la superficie dell’acquapublic static float elasticFactor: la costante elastica nella legge di Hooke, comune a tutte le molle che usiamo.public static float dampingFactor: un numero da 0 a 1 che indica quanto viene smorzato il movimento della molla, ovvero quanto velocemente la molla torna alla propria posizione originale
Per comodità, definiamo una classe Spring le cui istanze rappresenteranno una singola molla. Ogni molla deve memorizzare:
- Posizione (verticale)
- Posizione iniziale, intesa come posizione in cui la molla si trova a riposo.
- Velocità (verticale)
All’interno della classe Spring definiamo due metodi void:
public void ApplyForce(float force): lo useremo per applicare la forza a una specifica istanza di mollapublic void Update(): metodo che chiameremo per aggiornare la posizione della molla
Calcoliamo ora la relazione tra forza elastica, velocità e posizione della molla (d’ora in avanti, per posizione della molla indichiamo la posizione del punto più distante dalla posizione di riposo della molla)
$$F=-k\cdot\Delta x \quad F=ma$$
\(m\), la massa, possiamo considerarla pari a 1 in modo da semplificare i conti. Da qui otteniamo:
$$-k\cdot\Delta x = a$$
da cui
$$v_{n+1}=v_{n}-k\cdot\Delta x \cdot dt$$
e
$$P_{n+1}=P{n}+v_{n+1} \Delta \cdot dt$$
Dove \(v_{i}\) e \(P_{i}\) rappresentano rispettivamente la velocità e la posizione all’istante i.
Tutto ciò si riduce al seguente codice:
private class Spring {
public float position = 1, startPosition = 1, velocity = 0;
public void ApplyForce(float force) {
velocity += force;
}
public void Update() {
float positionDelta = startPosition - position;
float force = positionDelta * elasticFactor;
ApplyForce(force);
position += velocity;
velocity *= dampingFactor;
}
}Si noti che il codice in questione non include la moltiplicazione per Time.DeltaTime. Questo perché chiameremo Update() da FixedUpdate, che ha un deltaTime fisso. Nel caso in cui si voglia adattare questo sistema a un gioco più grande, in cui ci si aspetta di modificare Time.FixedDeltaTime, allora è conveniente aggiungerlo.
Introduciamo poi un metodo per generare le molle e un metodo per ripristinare la situazione di equilibrio iniziale, che tornerà utile dopo. Le istanze create dal generatore saranno aggiunte a una lista private List<Spring> che le conterrà.
private void generateSprings() {
for(int i = 0; i < springsCount; i++) {
springs.Add(new Spring());
}
}
private void resetSprings() {
for(int i = 0; i < springs.Count; i++) {
springs[i].velocity = 0f;
springs[i].position = springs[i].startPosition;
}
}Interagiamo con le molle
Vediamo ora di fare in modo che, quando un oggetto entra a contatto con l’acqua, applichi una forza alle molle mettendole in movimento. Utilizzeremo il movimento delle molle per deformare l’acqua.
public void displace(float x, float force = 0.15f) {
if(springs.Count == 0) return;
Vector3 localPos = transform.InverseTransformPoint(new Vector3(x, 0, 0));
float scaledX = Mathf.Clamp01(localPos.x) * (springs.Count - 1);
float rightWeight = scaledX % 1;
float leftWeight = 1 - rightWeight;
int leftIndex = Mathf.FloorToInt(scaledX);
int rightIndex = leftIndex + 1;
if(leftIndex >= 0) {
springs[leftIndex].ApplyForce(force * leftWeight);
}
if(rightIndex <= springs.Count - 1) {
springs[rightIndex].ApplyForce(force * rightWeight);
}
}Il metodo displace prende in input la posizione x a cui applicare la forza in input. La posizione è trasformata nello spazio locale e usata per trovare le due molle più vicine a cui applicare la forza. La forza applicata alle molle è proporzionale alla distanza tra x e la molla. Così facendo applicare il displacement a metà tra due molle equivale ad applicare due forze equivalenti alle due molle, la cui somma è pari alla forza originale.
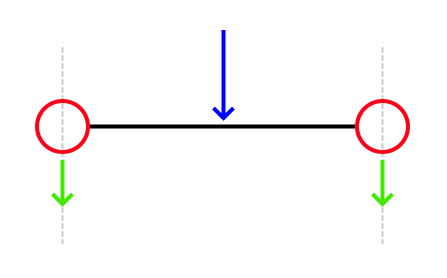
Questo sistema non tiene conto né della dimensione né della forma dell’oggetto che determina il displacement. In un’implementazione più completa, un’idea potrebbe essere inserire un parametro width che specifica l’area di deformazione spalmando la forza su una superficie arbitrariamente larga.
Possiamo gestire la chiamata a displace per gli oggetti che interagiscono con l’acqua in questo modo:
private void OnTriggerEnter2D(Collider2D collision) {
float force = defaultDisplacementForce;
Rigidbody2D rigidbody = collision.GetComponent<Rigidbody2D>();
if(rigidbody != null) {
float t = Mathf.Clamp01(rigidbody.linearVelocity.magnitude / maxImpactVelocity);
force = -Mathf.Lerp(defaultDisplacementForce, maxDisplacementForce, t);
}
displace(collision.transform.position.x , force);
}Definiamo due campi pubblici:
defaultDisplacementForce: la forza base (minima) da applicare in caso di collisionemaxDisplacementForce: la massima forza applicabile
Il codice in questione, quando un oggetto colpisce l’acqua, verifica se l’oggetto ha un componente Rigidbody2D, e in caso usa la sua velocità assoluta per modificare la forza da applicare. In caso contrario viene usata direttamente la forza di default.
Aggiorniamo la mesh
Ora che il movimento delle molle è implementato correttamente, possiamo aggiornare la mesh in relazione alla loro posizione.
Innanzitutto vediamo di creare due riferimenti: uno alla mesh e uno ai vertici che la costituiscono, e di generare rispettivamente la mesh e le molle:
private Vector3[] vertices;
private Mesh mesh;
private void Start() {
generateMesh();
mesh = GetComponent<MeshFilter>().mesh;
vertices = mesh.vertices;
generateSprings();
}Dopodiché dobbiamo aggiornare la mesh sulla base delle posizioni delle molle.
Vedremo due modi per farlo:
- Assegnando una molla a ciascun vertice della mesh
- Mantenendo indipendenza tra il numero di molle e la risoluzione della mesh
Il primo metodo è il più semplice, ma, come vedremo, anche il meno versatile.
Nel codice sopra abbiamo definito due variabili:
resolution(il numero di suddivisioni)springsCount(il numero di molle)
Per usare il primo metodo, facciamo in modo che resolution e springCount abbiano lo stesso esatto valore.
A quel punto, possiamo semplicemente assegnare a ogni vertice sulla superficie dell’acqua la posizione della rispettiva molla.
Ecco come:
//METODO 1: resolution = springsCount
private void FixedUpdate() {
if(vertices == null || springs == null) return;
for(int i = 0; i < springs.Count; i++) {
springs[i].Update();
}
updateMeshFromSprings();
}In FixedUpdate aggiorniamo le posizioni di ogni molla ciclando sulla lista di molle e chiamando Update() su ogni istanza. Dopodiché chiamiamo un nuovo metodo updateMeshFromSprings(), responsabile dell’aggiornamento della mesh in base alla posizione delle molle. Questo metodo è implementato come segue:
//METODO 1: resolution = springsCount
private void updateMeshFromSprings() {
for(int i = 0; i < resolution; i++) {
int topIndex = i * 2 + 1;
vertices[topIndex].y = springs[i].position;
}
mesh.vertices = vertices;
mesh.RecalculateBounds();
mesh.RecalculateNormals();
}Molto semplicemente, assegnamo alla coordinata y di ciascun vertice la posizione della rispettiva molla. Questo richiede che il numero di molle sia pari al numero di suddivisioni, altrimenti ci sarebbero vertici senza molle.
Usciti dal ciclo, assegnamo i nuovi vertici alla mesh.
Possiamo creare uno spawner di oggetti in modo da verificare che tutto funzioni correttamente. Creiamo un oggetto vuoto in Unity, chiamiamolo SphereSpawner, e assegnamogli il seguente script:
using UnityEngine;
public class SphereSpawner : MonoBehaviour
{
public Sprite spriteImage;
void Update()
{
if(Input.GetMouseButtonDown(0)) {
SpawnAtMouse();
}
}
void SpawnAtMouse() {
Vector3 mouseScreen = Input.mousePosition;
Vector3 worldPos = Camera.main.ScreenToWorldPoint(mouseScreen);
worldPos.z = 0f;
GameObject sphere = new GameObject("Sphere");
sphere.transform.position = worldPos;
SpriteRenderer renderer = sphere.AddComponent<SpriteRenderer>();
if(spriteImage != null) {
renderer.sprite = spriteImage;
}
sphere.AddComponent<CircleCollider2D>();
sphere.AddComponent<Rigidbody2D>();
}
}In questo modo, ogni volta che cliccheremo il tasto sinistro del mouse, comparirà uno sprite con Rigidbody in corrispondenza del puntatore.
A questo punto dovreste vedere le onde formarsi quando una sfera colpisce la superficie dell’acqua. L’unico problema è che le onde non si propagano, ma rimangono fisse nella loro posizione originale.
Prima di vedere come implementare il secondo metodo di aggiornamento della mesh, è conveniente lavorare alla propagazione delle onde.
Propagazione delle onde
Per fare in modo che le onde si propaghino lungo la superficie dell’acqua, dobbiamo immaginare che ciascuna molla, spostandosi dalla propria posizione di equilibrio, tiri con sé le molle vicine, che vedranno variare la loro velocità e posizione sulla base della molla in movimento.
Definiamo allora una variabile pubblica spreadFactor, che indica quanto il movimento di ogni molla si propaga alle molle vicine. Questo valore andrà tenuto basso, perché altrimenti si corre il rischio di avere un sistema in cui, se si applica una forza a una molla, le molle vicine subiscono una forza superiore. Un sistema del genere è instabile e non funzionante.
Nel FixedUpdate, definiamo due liste di float: leftDeltas e rightDeltas. Ognuna di queste liste manterrà, in ogni indice, la differenza di posizione tra la molla con quell’indice e la molla rispettivamente a sinistra e a destra.
Quello che dobbiamo fare è popolare queste liste e, contemporaneamente, aggiornare le velocità delle molle in relazione alle loro differenze di posizione. Dopodiché, in un secondo passaggio, modificheremo la posizione delle molle in base ai valori memorizzati in leftDeltas e rightDeltas.
Questo equivale ad applicare una forza proporzionale alla differenza di posizione tra le varie molle, andando così a “spalmare” la forza iniziale lungo l’intera superficie dell’acqua.
private void FixedUpdate() {
if(vertices == null || springs == null) return;
for(int i = 0; i < springs.Count; i++) {
springs[i].Update();
}
updateMeshFromSprings();
for(int i = 0; i < springs.Count; i++) {
if(i > 0) {
leftDeltas[i] = spreadFactor * (springs[i].position - springs[i - 1].position);
springs[i - 1].velocity += leftDeltas[i];
}
if(i < springs.Count - 1) {
rightDeltas[i] = spreadFactor * (springs[i].position - springs[i + 1].position);
springs[i + 1].velocity += rightDeltas[i];
}
}
for(int i = 0; i < springs.Count; i++) {
if(i > 0) {
springs[i - 1].position += leftDeltas[i];
}
if(i < springs.Count - 1) {
springs[i + 1].position += rightDeltas[i];
}
}
}Questo metodo propaga la forza una molla alla volta. Per velocizzare la propagazione possiamo aggiungere una variabile wavePropagationPasses che indica quante volte ripetere la propagazione:
for(int j = 0; j < wavePropagationPasses; j++) {
for(int i = 0; i < springs.Count; i++) {
if(i > 0) {
leftDeltas[i] = spreadFactor * (springs[i].position - springs[i - 1].position);
springs[i - 1].velocity += leftDeltas[i];
}
if(i < springs.Count - 1) {
rightDeltas[i] = spreadFactor * (springs[i].position - springs[i + 1].position);
springs[i + 1].velocity += rightDeltas[i];
}
}
for(int i = 0; i < springs.Count; i++) {
if(i > 0) {
springs[i - 1].position += leftDeltas[i];
}
if(i < springs.Count - 1) {
springs[i + 1].position += rightDeltas[i];
}
}
}Volendo possiamo fermarci qui. Tuttavia, poiché l’aggiornamento della mesh richiede che il numero di molle sia uguale alla risoluzione, una risoluzione maggiore automaticamente implica una propagazione più lenta delle onde, dato che in ogni FixedUpdate la propagazione coinvolge wavePropagationPasses molle.
Ci sono due modi per risolvere: uno è impostare wavePropagationPasses come frazione del numero di molle, ad esempio wavePropagationPasses = springs.Count / 8.
Questo sistema, tuttavia, fa assumere al loop di propagazione delle onde una complessità computazionale pari a \(O(n^2)\), il che non è ottimale.
Una soluzione migliore è quella di eliminare il vincolo che forza il numero di molle ad essere pari al numero di vertici in superficie, e rivedere la generazione della mesh per permettere di avere poche molle anche con un gran numero di vertici.
Aggiornamento della mesh tramite spline Catmull-Rom
Per fare in modo che le onde siano generate da un numero di molle inferiore al numero di vertici in superficie possiamo ragionare per interpolazione. Supponiamo di avere 500 vertici e 5 molle.
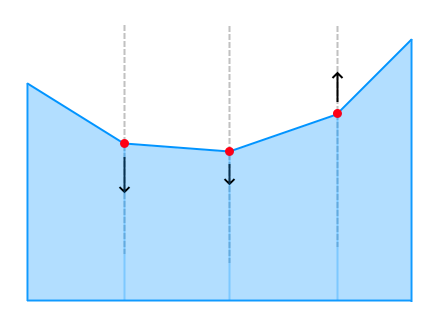
Per poter associare ogni vertice a una posizione nello spazio, dobbiamo trovare una funzione che interpoli le 5 molle in modo naturale. Questo significa trovare una funzione \(f(x)\) che in corrispondenza delle molle assuma come valore la loro posizione sull’asse y, e negli altri punti un valore che indica la y che devono assumere i vertici per seguire l’andamento delle molle:

La curva che useremo si chiama Spline Catmull-Rom. Si tratta di una funzione polinomiale definita a tratti, ovvero di una sequenza di polinomi legati insieme in modo che il loro grafico appaia coeso e continuo.
Un singolo polinomio usato per costruire la spline è un polinomio \(P(x)\) di terzo grado, ovvero un polinomio nella forma \(P(x)=ax^3+bx^2+cx+d\), ma con le seguenti caratteristiche:
- \(P(c_i)=y_i\): il polinomio passa per il primo punto di controllo \(c_i\)
- \(P(c_{i+1})=y_{i+1}\): il polinomio passa per il secondo punto di controllo \(c_{i+1}\)
- \(P'(c_i)=(y_{i+1}-y_{i-1}) / (c_{i+1} – c_{i-1})\): il valore della derivata prima nel primo punto di controllo è pari al coefficiente della retta che collega i due punti adiacenti
- \(P'(c_{i+1})=(y_{i+2}-y_{i+1}) / (c_{i+2} – c_{i})\): il valore della derivata prima nel secondo punto di controllo è pari al coefficiente della retta che collega i due punti adiacenti
Risolvendo il corrispettivo sistema lineare possiamo trovare i coefficienti del polinomio espressi in funzione delle posizioni di 4 molle:
\begin{aligned}
a &= \frac{1}{2}\left(-p_0 + 3p_1 – 3p_2 + p_3\right), \\
b &= \frac{1}{2}\left( 2p_0 – 5p_1 + 4p_2 – p_3\right), \\
c &= \frac{1}{2}\left(-p_0 + p_2\right),\\
d &= p_1
\end{aligned}
Dove \(p_i\) indica la posizione della i-esima molla.
Possiamo allora definire un metodo SampleSplineAt(float localX) usato per ottenere il valore dalla spline a una certa posizione. La posizione in questione è espressa in un range \([0,1]\) che rappresenta la larghezza dell’intero specchio d’acqua.
Il metodo è implementato come segue:
private float SampleSplineAt(float localX) {
int segmentCount = springsCount - 1;
int i = Mathf.FloorToInt(localX * segmentCount);
i = Mathf.Clamp(i, 1, springsCount - 3);
float u = localX * segmentCount - i;
float p0 = springs[i - 1].position;
float p1 = springs[ i ].position;
float p2 = springs[i + 1].position;
float p3 = springs[i + 2].position;
return 0.5f * (u * (u * (u * (-p0 + 3f * p1 - 3f * p2 + p3) +
(2f * p0 - 5f * p1 + 4f * p2 - p3)) +
(-p0 + p2)) +
(2f * p1));
}Si noti il modo in cui è scritto il polinomio. In questo caso è infatti possibile usare la Regola di Horner per ridurre il numero di operazioni necessarie per calcolare il polinomio.
L’algoritmo di Horner, infatti, permette di esprimere polinomi nella forma
$${\displaystyle P_{N}(x)=a_{0}x^{N}+a_{1}x^{N-1}+…+a_{N-1}x+a_{N}}$$
Come
$${\displaystyle P_{N}(x)=a_{N}+x(a_{N-1}+x(a_{N-2}+\ldots +x(a_{1}+a_{0}x)\ldots ))}$$
Essenzialmente, nidificando l’espressione, è possibile usare un numero minore di moltiplicazioni rispetto al metodo tradizionale. Siccome chiameremo questa funzione moltissime volte, questa ottimizzazione è sensata.
Ora possiamo aggiornare la mesh in questo modo:
private void updateMeshFromSprings() {
float deltaX = 1 / (float)resolution;
float localX = 0;
for(int i = 0; i < resolution; i++) {
int topIndex = i * 2 + 1;
vertices[topIndex].y = SampleSplineAt(localX);
localX += deltaX;
}
mesh.vertices = vertices;
mesh.RecalculateBounds();
mesh.RecalculateNormals();
}Sleeping system
Supponiamo ora di utilizzare questo sistema in un gioco vero e proprio, e di avere vari specchi d’acqua in un’unica schermata. Supponiamo ora che il giocatore sia in grado di interagire solamente con un ristretto sottoinsieme di questi specchi d’acqua. Che cosa accade? I calcoli fisici e il sampling delle spline continuano anche per gli oggetti d’acqua che sono completamente privi di deformazioni in corso. Questo è uno spreco.
Per ottimizzare tutto ciò possiamo introdurre un sistema di sleeping.
Aggiungiamo una variabile privata booleana isAwake, che indica se l’oggetto acqua è “dormiente” o meno.
Vogliamo che l’acqua si risvegli quando un oggetto entra in collisione, e che si addormenti quando le onde si sono completamente dissipate.
Per fare ciò, possiamo impostare isAwake a true quando un oggetto entra in collisione, e prevedere un intervallo di controllo periodico che valuta se è necessario addormentare l’acqua in base a quante onde sono presenti.
private bool isAwake = false;
private void Start() {
// ...
StartCoroutine(checkDisplacementEnd());
}
private void FixedUpdate() {
if(vertices == null ||
springs == null ||
isAwake == false) return;
//...
}
IEnumerator checkDisplacementEnd() {
const float CHECK_INTERVAL = 2.5f;
const float MIN_VELOCITY_THRESHOLD = 0.00025f;
yield return new WaitForSeconds(CHECK_INTERVAL);
float maxAbsoluteVelocity = 0;
for(int i = 0; i < springs.Count; i++) {
if(Mathf.Abs(springs[i].velocity) > maxAbsoluteVelocity) {
maxAbsoluteVelocity = Mathf.Abs(springs[i].velocity);
}
}
if(maxAbsoluteVelocity < MIN_VELOCITY_THRESHOLD) {
isAwake = false;
resetSprings();
}
StartCoroutine(checkDisplacementEnd());
}Ogni CHECK_INTERVAL secondi si cerca la massima velocità, in valore assoluto, tra tutte le molle. Se questa velocità è inferiore di MIN_VELOCITY_THRESHOLD si assume che l’acqua non abbia onde e che sia possibile “addormentarla”.
Quando isAwake è true, in FixedUpdate abbiamo un early return che evita di aggiornare le molle e di fare il sampling della spline.
Shader
Per colorare l’acqua in maniera convincente possiamo usare lo shader graph:
- Usiamo due mappe Voronoi elevate a potenza e con offset temporale per simulare delle caustiche.
- Utilizziamo un semplice gradiente per dare colore all’acqua in base alla profondità
- Usando l’UV, definiamo un offset dalla superficie entro il quale l’acqua si colora di bianco per avere un effetto “contorno”
- Sfruttando la derivata verticale sull’UV, implementiamo l’oscuramento dell’acqua in corrispondenza delle zone a più alta variazione d’altezza.
Lo shader graph risultante è il seguente:
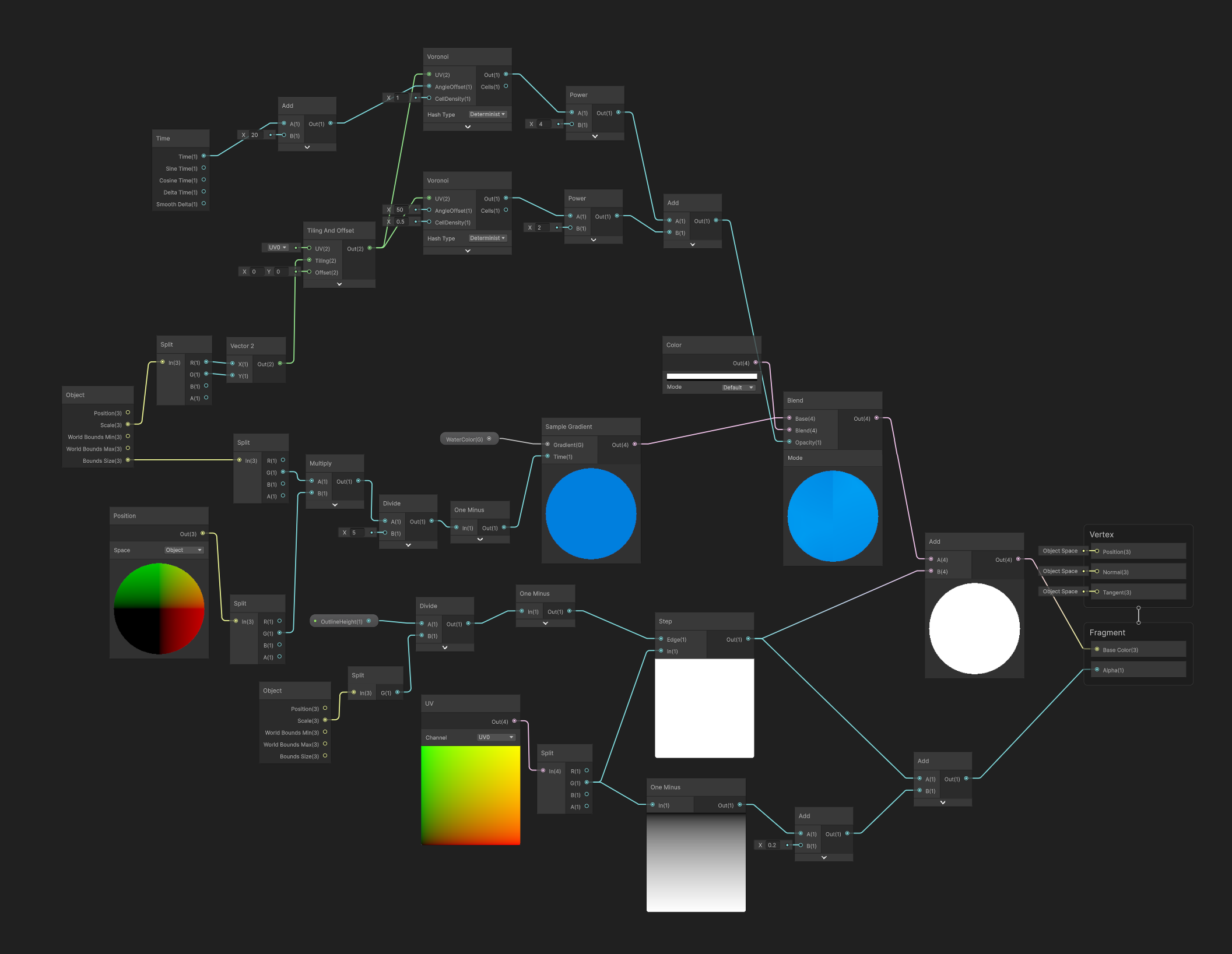
Il risultato finale che si ottiene è il seguente:
Codice finale
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.Profiling;
using UnityEngine.SocialPlatforms;
public class InteractiveWater : MonoBehaviour
{
private Vector3[] vertices;
private Mesh mesh;
public int resolution = 12;
public int springsCount = 20;
public float defaultDisplacementForce = 0.5f;
public float maxDisplacementForce = 5f;
public float maxImpactVelocity = 100f;
public int wavePropagationPasses = 8;
public static float elasticFactor = 0.02f;
public static float dampingFactor = 0.99f;
private float[] leftDeltas;
private float[] rightDeltas;
public float spreadFactor = 0.02f;
private bool isAwake = false;
private List<Spring> springs = new List<Spring>();
private class Spring {
public float position = 1, startPosition = 1, velocity = 0;
public void ApplyForce(float force) {
velocity += force;
}
public void Update() {
float positionDelta = startPosition - position;
float force = positionDelta * elasticFactor;
ApplyForce(force);
position += velocity;
velocity *= dampingFactor;
}
}
private void Start() {
generateMesh();
mesh = GetComponent<MeshFilter>().mesh;
vertices = mesh.vertices;
generateSprings();
leftDeltas = new float[springs.Count];
rightDeltas = new float[springs.Count];
StartCoroutine(checkDisplacementEnd());
}
private void FixedUpdate() {
if(vertices == null || springs == null || isAwake == false) return;
for(int i = 0; i < springs.Count; i++) {
springs[i].Update();
}
updateMeshFromSprings();
for(int j = 0; j < wavePropagationPasses; j++) {
for(int i = 0; i < springs.Count; i++) {
if(i > 0) {
leftDeltas[i] = spreadFactor * (springs[i].position - springs[i - 1].position);
springs[i - 1].velocity += leftDeltas[i];
}
if(i < springs.Count - 1) {
rightDeltas[i] = spreadFactor * (springs[i].position - springs[i + 1].position);
springs[i + 1].velocity += rightDeltas[i];
}
}
for(int i = 0; i < springs.Count; i++) {
if(i > 0) {
springs[i - 1].position += leftDeltas[i];
}
if(i < springs.Count - 1) {
springs[i + 1].position += rightDeltas[i];
}
}
}
}
private void generateMesh() {
Mesh mesh = new Mesh();
Vector3[] vertices = new Vector3[(resolution + 1) * 2];
int[] triangles = new int[resolution * 6];
Vector2[] uv = new Vector2[vertices.Length];
for(int x = 0; x <= resolution; x++) {
int index = x * 2;
float normalizedX = (float)x / resolution;
vertices[index] = new Vector3(normalizedX, 0, 0);
vertices[index + 1] = new Vector3(normalizedX, 1, 0);
uv[index] = new Vector2(normalizedX, 0);
uv[index + 1] = new Vector2(normalizedX, 1);
}
int triangleIndex = 0;
for(int x = 0; x < resolution; x++) {
int bottomLeft = x * 2;
int topLeft = bottomLeft + 1;
int bottomRight = bottomLeft + 2;
int topRight = bottomLeft + 3;
triangles[triangleIndex++] = bottomLeft;
triangles[triangleIndex++] = topLeft;
triangles[triangleIndex++] = topRight;
triangles[triangleIndex++] = bottomLeft;
triangles[triangleIndex++] = topRight;
triangles[triangleIndex++] = bottomRight;
}
mesh.vertices = vertices;
mesh.uv = uv;
mesh.triangles = triangles;
mesh.RecalculateNormals();
mesh.RecalculateBounds();
GetComponent<MeshFilter>().mesh = mesh;
}
private void updateMeshFromSprings() {
float deltaX = 1 / (float)resolution;
float localX = 0;
for(int i = 0; i < resolution; i++) {
int topIndex = i * 2 + 1;
vertices[topIndex].y = SampleSplineAt(localX);
localX += deltaX;
}
mesh.vertices = vertices;
mesh.RecalculateBounds();
mesh.RecalculateNormals();
}
private void generateSprings() {
for(int i = 0; i < springsCount; i++) {
springs.Add(new Spring());
}
}
private void resetSprings() {
for(int i = 0; i < springs.Count; i++) {
springs[i].velocity = 0f;
springs[i].position = springs[i].startPosition;
}
updateMeshFromSprings();
}
public void displace(float x, float force = 0.15f) {
if(springs.Count == 0) return;
isAwake = true;
Vector3 localPos = transform.InverseTransformPoint(new Vector3(x, 0, 0));
float scaledX = Mathf.Clamp01(localPos.x) * (springs.Count - 1);
float rightWeight = scaledX % 1;
float leftWeight = 1 - rightWeight;
int leftIndex = Mathf.FloorToInt(scaledX);
int rightIndex = leftIndex + 1;
if(leftIndex >= 0) {
springs[leftIndex].ApplyForce(force * leftWeight);
}
if(rightIndex <= springs.Count - 1) {
springs[rightIndex].ApplyForce(force * rightWeight);
}
}
private void OnTriggerEnter2D(Collider2D collision) {
float force = defaultDisplacementForce;
Rigidbody2D rigidbody = collision.GetComponent<Rigidbody2D>();
if(rigidbody != null) {
float t = Mathf.Clamp01(rigidbody.linearVelocity.magnitude / maxImpactVelocity);
force = -Mathf.Lerp(defaultDisplacementForce, maxDisplacementForce, t);
}
displace(collision.transform.position.x , force);
}
IEnumerator checkDisplacementEnd() {
const float CHECK_INTERVAL = 2.5f;
const float MIN_VELOCITY_THRESHOLD = 0.00025f;
yield return new WaitForSeconds(CHECK_INTERVAL);
float maxAbsoluteVelocity = 0;
for(int i = 0; i < springs.Count; i++) {
if(Mathf.Abs(springs[i].velocity) > maxAbsoluteVelocity) {
maxAbsoluteVelocity = Mathf.Abs(springs[i].velocity);
}
}
if(maxAbsoluteVelocity < MIN_VELOCITY_THRESHOLD) {
isAwake = false;
resetSprings();
}
StartCoroutine(checkDisplacementEnd());
}
private float SampleSplineAt(float localX) {
int segmentCount = springsCount - 1;
int i = Mathf.FloorToInt(localX * segmentCount);
i = Mathf.Clamp(i, 1, springsCount - 3);
float u = localX * segmentCount - i;
float p0 = springs[i - 1].position;
float p1 = springs[ i ].position;
float p2 = springs[i + 1].position;
float p3 = springs[i + 2].position;
return 0.5f * (u * (u * (u * (-p0 + 3f * p1 - 3f * p2 + p3) +
(2f * p0 - 5f * p1 + 4f * p2 - p3)) +
(-p0 + p2)) +
(2f * p1));
}
}

Lascia un commento